数据结构--树（BST）

​ 树是一种简单的数据结构，其插入查找的速度都相对均匀：O(logN)，这里用到的主要是二叉查找树binary search tree。

• 了解树在文件系统里的应用
• 计算算术表达式的值，如中缀表达式等
• 树是如何实现以O(logN)的平均时间进行查找操作，以及最坏时间O(logN)。

树的基本模型

树的构成：

​ 每棵树都有根节点和数个非空子树组成

​ 一棵树是N个节点和N-1条边的集合，原因很简单，除了根节点之外，每个节点都与其父节点有一条边相连接。

树的路径长度，高度与深度：

• 长度：n1-nk的路径上的边的条数，树上的任意一个节点都有到跟的路径
• 高度：任意ni节点到根节点的唯一路径的长度看作为该节点的高度，即节点越往下，高度越大，与根节点离得越远高度越大！
• 深度：以ni为当前子树的根节点，向下寻找树叶，由该节点到树叶的路径的长度，记作该节点的高度

不管是深度也好，高度也好，基本上都是相对于你选择的根节点而言的，并不是完全固定不变的，是一个相对的数值，不过求出每一个高度和深度的路径都是唯一的

树的代码实现

树的节点声明：

typedef struct TreeNode *PtrToNode;
struct TreeNode{
    ElementType Element; 	//抽象数据类型，定义树节点存放的数据
    PtrToNode FirstChild;	//第一个子树的指针（第一儿子）
    PtrToNode NextChild;	//下一个子树的指针（下一个兄弟）
}

因为实现并不知道子树的个数，所以直接在声明里指定个数是不理智的，所以应该换一种方式，使用链表来存储树，具体的图明天再来画吧！

树的遍历及应用：

UNIX文件系统：文件树的遍历

ListD(DirectryOfFile D,int Depth){ 	//文件目录，目录深度
	//D是一个合法的文件入口那么就进行遍历
    if(D is a legitimate entry){	
        for (child C : D){
            ListD(C,Depth+1);
        }
    }
}

​ 经过几次递归之后就可以完全打印出文件目录。

遍历方式：

1. 先序遍历：

   在先序遍历中，对节点的处理在处理儿子结点之前！下面是线序遍历的图例，节点的数字代表遍历的顺序。

   

2. 后序遍历：

   在后序遍历中，对节点的处理在处理儿子节点之后！下面是后序遍历的图例。

   

   一些个人理解：不管是先序遍历还是后序遍历还是层序遍历，其本质都是一件事情：递归，通过一种相似的查找方式打印出需要遍历的树中所有的节点。

二叉树

定义：

​ 二叉树是一种树，其中每个节点的子节点不得多于两个。二叉树的一个重要性质是平均二叉树的深度要比N要小得多为O($\sqrt{N} $),而二叉查找树的平均深度是O($\log{N}$)。

实现：

typedef struct TreeNode *PtrToNode;
typedef struct PtrNode Tree;
struct TreeNode{
    ElementType Element;	//节点的值
    Tree left;	//左子树
    Tree right;	//右子树
}

每个有N个节点的二叉树都有N+1个NULL空指针

表达式树：

​ 利用二叉树实现中缀表达式，前缀表达式等等，还需要结合队列来实现整个数据结构！
​

• 表达式树的树叶表示表达式的操作数，比如变量或者常量，而其他的根结点代表操作符。
• 所有的操作符都是二元操作符。
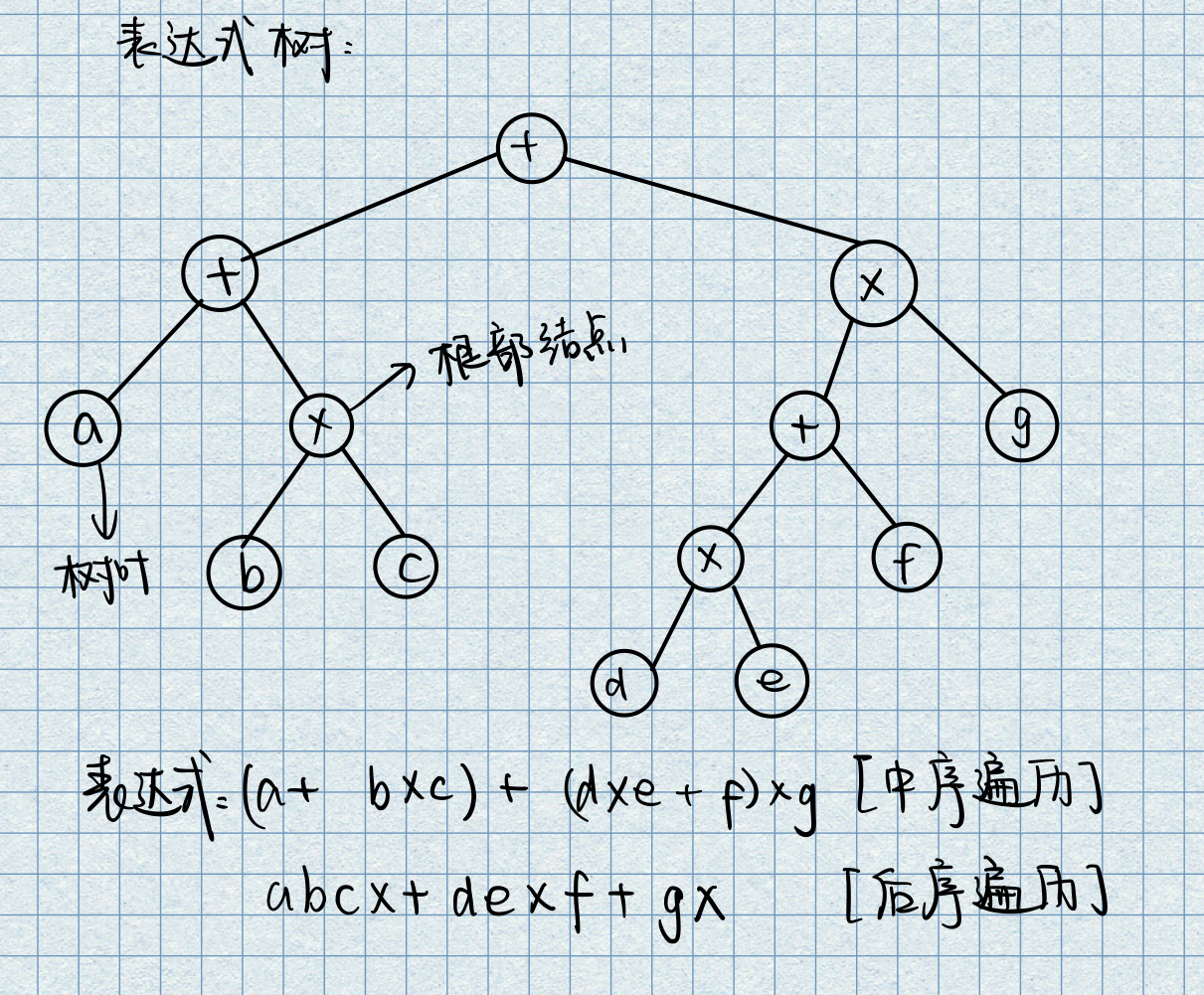
  下面给出一个例子：

  左子树a+(b*c)。右子树(((d*e）+f)*g)

  

二叉查找树

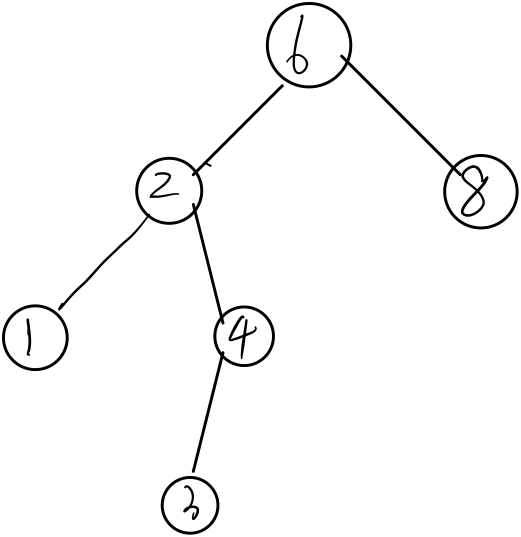
• 概念：对于二叉查找树中的任意节点X，它的左子树所有关键字值小于该节点所代表的关键字的值，而其右子树的所有关键字的值大于X的关键字值。因此该二叉树的所有元素都可以用某种统一的方式排序。

这里有一个二叉查找树的查找时间复杂度的计算问题，我之前上课的时候没怎么想明白，刚刚上网查了一下发现是我智障了。
其实二叉查找树的原理跟二分法的原理是完全一样的：在N个数据的数组里取第Ｎ／2个元素，将这个元素与输入元素进行对比，如果小与输入元素就去该节点的右子树中查找，如果大于就去左子树。假设查找的次数为x次，那么表达式就是：N*（$1/2$）^X = 1，即最坏情况是查找到首尾元素，最后即可得出查找的时间复杂度为O($\log{N}$).

• 增删查改：
  1. Insert
  2. Delete：删除操作是相对困难的一部分，这里仅仅讨论处理有两个儿子的操作。
     • 一般的删除策略是用其右子树的最小数据（右子树的最左侧的那个节点）代替该节点的数据，并递归地删除那个（被替换掉的）节点。由于该节点不可能有左子树，所以第二次删除要容易。接下来是一个例子
     • 
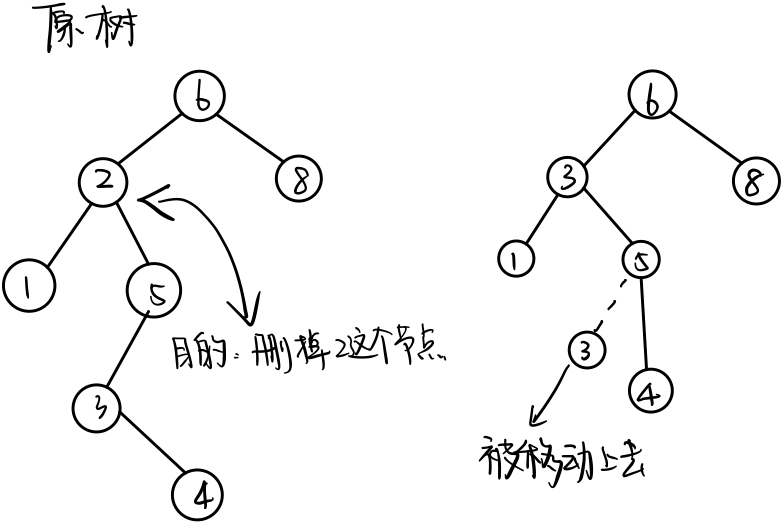
     • 然后被移动的关键字3像之前删除2一样删除！