数据结构入门？这一篇就够了
发表Code0次访问

数据结构入门？这一篇就够了

算法分析

运行时间的计算分析

上界：$O(f(N))$

下界：$Ω(g(N))$

准确表达则为：$Θ(h(N))$

也就是说都是一个关于N的函数！

这么做的目的是为了比较两个算法的相对增长速率

求解算法时间复杂度的步骤

  1. 找出算法中的基本语句；

　　算法中执行次数最多的那条语句就是基本语句，通常是最内层循环的循环体。

  1. 计算基本语句的执行次数的数量级；

　　只需计算基本语句执行次数的数量级，这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可，可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析，并且使注意力集中在最重要的一点上：增长率。

  1. 用大Ο记号表示算法的时间性能。

　　将基本语句执行次数的数量级放入大Ο记号中。

  1. 可以忽略末尾带上的常数项
1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 求数组中的子序列的和的最大值
int MaxSubsequenceSum(const int A[],int N){
    int maxSum = 0;
    int tempSum = 0;
    for(int i = 0;i < N;i++){
        tempSum += A[i];
        if(tempSum > maxSum){
            maxSum = tempSum;
        }else if(tempSum < 0){
            tempSum = 0;
        }
    }
    return maxSum;
}

复杂度函数的运算规则

抽象数据类型ADT

表

表分为两种，顺序表与链表。其中顺序表要求系统给其分配的内存单元是连续的，因此，顺序表的访问时间可以做到线性时间，第二种是链表，链表不要求连续的内存空间，但其中的每一块都是与其他链表节点耦合的。

顺序表

即数组，内存地址连续。

访问时为线性访问，速度较快。插入删除时代价较大，因为需要更改其后所有元素的信息才能维持当前的顺序表。

链表

在C语言中是通过建立结构体然后存储指针的方式来进行访问的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 邻接表中表的顶点
typedef struct _VNode
{
    int index;          // 顶点信息
    ENode *firstEdge; // 指向第一条依附该顶点的弧
} VNode;

// 邻接表
typedef struct _LGraph
{
    int vexNum; // 图的顶点的数目
    int edgNum; // 图的边的数目
    VNode vexs[MAX];
} LGraph;

代码片段

循环链表
双向链表
双向循环链表

栈

特点：先进后出FILO

只需要一个指针就可以利用链表来实现栈的数据结构，在栈中只有栈顶可以出入数据，栈底的数据只有等其他数据都出去了才能被弹出

两个栈操作：PUSH POP

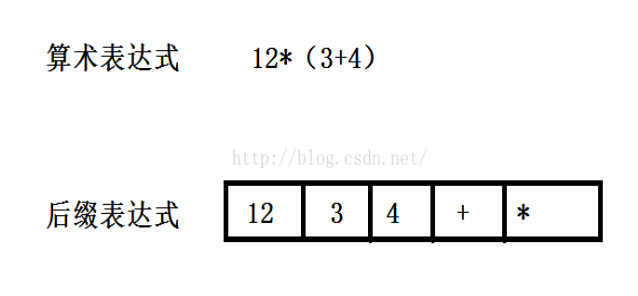
实例：使用栈数据结构来实现后缀表达式

队列

特点：先进先出FIFO

对于队列而言，有两个口可以与外界交换数据，分别是队列头和队列尾部。

只允许在队列尾部入队，在队列头部出队。

两个操作：Enqueue Dequeue

树

二叉树

二叉查找树

之前写的二叉树博客

本地

AVL树

AVL树是带有平衡条件的二叉查找树。

平衡条件必须要相对容易保持，而且必须保证树的深度是$O(logN)$，那么在AVL树中，就是保证节点的左右子树的高度之差小于2，即只能为1或者0 。

下面是AVL树插入的C语言实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
#include <stdio.h>
#include <stdlib.h>
#define MAX(a,b) (a > b) ? (a) : (b)
/**
 * AVL树的结构体定义
 * */
typedef struct AVLTreeNode
{   
    int data;   //节点存储的值
    int height; //当前节点的高度
    struct AVLTreeNode *leftChild;  //左儿子
    struct AVLTreeNode *rightChild; //右儿子
}Node,*AVLTree;
/***
 * @param data 存储的数据
 * @param left 左儿子
 * @param right 右儿子
 * */
static Node *createAVLTreeNode(int data,Node *left,Node *right){
    // 为这个新的节点开辟内存空间
    Node *node;
    if (((node = (Node *)malloc(sizeof(Node))) == NULL)){
        return NULL;
    }
    // 为这个node赋初值
    node->data = data;
    // 空子树的高度为0
    node->height = 0;
    node->leftChild = left;
    node->rightChild = right;

    return node;
}
// 获取节点的高度
int getHeightOfNode(Node *node){
    return (node==NULL) ? 0 : node->height;
}
/*
 * LL：左左对应的情况(左单旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* leftLeftRotation(AVLTree k2){
    AVLTree k1;

    k1 = k2->leftChild;
    // k2与k1的右子树进行互换
    k2->leftChild = k1->rightChild;
    k1->rightChild = k2;

    k2->height = MAX( getHeightOfNode(k2->leftChild), getHeightOfNode(k2->rightChild)) + 1;
    k1->height = MAX( getHeightOfNode(k1->leftChild), k2->height) + 1;
    // 旋转完成之后的根节点是k1，即k1上浮了而原本的k2下沉为k1的儿子了
    return k1;
}
/*
 * RR：右右对应的情况(右单旋转)。
 *
 * 返回值：旋转后的根节点
 */
static Node* rightRightRotation(AVLTree k2){
    AVLTree k1;

    k1 = k2->rightChild;
    // k2与k1的右子树进行互换
    k2->rightChild = k1->leftChild;
    k1->leftChild = k2;

    k2->height = MAX( getHeightOfNode(k2->leftChild), getHeightOfNode(k2->rightChild)) + 1;
    //此时的k2为k1的左儿子，所以只需要比较k2和k1的右儿子的高度就好了
    k1->height = MAX( getHeightOfNode(k1->rightChild), k2->height) + 1;
    // 旋转完成之后的根节点是k1，即k1上浮了而原本的k2下沉为k1的儿子了
    return k1;
}
/**
 * 
 * LR
 * 相当于进行了一次RR旋转一次LL旋转。
 * */
static Node *leftRightRotation(Node *k3){
    //先对k3的左子树进行RR旋转，再对旋转后的k3进行LL旋转
    k3->leftChild = rightRightRotation(k3->leftChild);
    return leftLeftRotation(k3);
}
/**
 * 
 * RL
 * 相当于进行了一次LL旋转一次RR旋转。
 * */
static Node *rightLeftRotation(Node *k3){
    //先对k3的右子树进行LL旋转，再对旋转后的k3进行RR旋转
    k3->rightChild = leftLeftRotation(k3->rightChild);
    return rightRightRotation(k3);
}
/**
 * 传入要插入的树
 * 传入要插入的数据
 * 返回更新后的树的根节点
 * */
Node *insertIntoAVLTree(AVLTree tree,int data){
    // 如果树是一个空树
    if (tree == NULL){
        // 那么就建立一个空节点
        tree = createAVLTreeNode(data,NULL,NULL);
        // 如果创建失败的话
        if (tree == NULL){
            printf("Create Node Failed");
        }
        
    }
    if (data < tree->data)//如果要插入的数值比根节点的值要小，那么就插入到其左子树中
    {
        // 然后递归调用插入方法，直到找到一个空节点再插入！
        tree->leftChild = insertIntoAVLTree(tree->leftChild,data);
        // 由于是插入到左子树中，因此只可能是左子树的高度大于右子树的高度
        if (getHeightOfNode(tree->leftChild) - getHeightOfNode(tree->rightChild) == 2)
        {
            // 如果需要插入的值根节点的左子树还要小那么说明插入到了左子树的左侧，那就可以判断此时的不平衡状态为左左LL，调用LL旋转即可
            if (data < tree->leftChild->data)
            {
                tree->leftChild = leftLeftRotation(tree->leftChild);
            }else   // 否则就说明大于这个节点的值，插入到在左子树的右儿子上，调用LR旋转
            {
                tree->leftChild = leftRightRotation(tree->leftChild);
            }
        }
    }
    else if (data > tree->data)
    {//如果要插入的数值比根节点的值要大，那么就插入到其由子树中
        tree->rightChild = insertIntoAVLTree(tree->rightChild,data);
        if (getHeightOfNode(tree->rightChild) - getHeightOfNode(tree->leftChild) == 2)// 由于插入到右子树中那么就是只有可能右子树的高度大于左子树的高度
        {
            if (data > tree->rightChild->data)
            {
                tree->rightChild = rightRightRotation(tree->rightChild);
            }else
            {
                tree->rightChild = rightLeftRotation(tree->rightChild);
            }
        }
    }else
    {
        printf("Don't Insert The Same Node");
    }
    // 更新根节点的高度
    if (((MAX(getHeightOfNode(tree->leftChild),getHeightOfNode(tree->rightChild))) == 0) && (tree->leftChild != NULL || tree->rightChild != NULL))
    {
        // 其子节点全部都是叶子节点
        // 说明两个子树至少存在一个，那么这个根节点的高度就是1
        tree->height = 1;
    }else if (tree->leftChild == NULL && tree->rightChild == NULL)
    {
        // 如果两个子树都不存在那么说明这个节点就是叶子节点，直接返回就好
        return tree;
    }else
    {
        tree->height = (MAX(getHeightOfNode(tree->leftChild),getHeightOfNode(tree->rightChild))) + 1;
    }
    
    return tree;
}

int main()
{
    Node *root = createAVLTreeNode(10,NULL,NULL);
    Node *left = createAVLTreeNode(6,NULL,NULL);
    Node *right = createAVLTreeNode(13,NULL,NULL);
    root->leftChild = left;
    root->rightChild = right;
    root = insertIntoAVLTree(root,5);
    // 此时接着插入值为3的节点就会破坏AVL树的平衡条件
    root = insertIntoAVLTree(root,3);
    printf("Hello world!\n");
    return 0;
}

伸展树

B-树

B-树是为了磁盘存储而设计的一种多叉树，是多叉平衡查找树

用阶数来定义B-树：

B 树又叫平衡多路查找树。一棵m阶的B 树具有以下性质：

  1. 每个节点的子节点个数为
    $$
    M/2 ≤ N ≤ M
    $$

  2. 并且B树的全部叶子节点在同一高度上

  3. 根节点至少有两个子树

  4. 由$N$ 个子树的节点一定含有$N-1$个关键字

  5. Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。

  6. Pi为指向子树根的接点，且指针P(i-1)指向子树中所有结点的关键字均小于Ki，但都大于K(i-1)。–指针域的定义

树的遍历

先序遍历，后序遍历。其中的前/后都是儿子节点相对于父节点而言的！

  • 先序遍历：对根节点的处理在儿子节点的处理之前
  • 后序遍历：对儿子节点的处理在根节点的处理之前
  • 中序遍历：先遍历左子树再遍历根节点最后遍历右子树。可以生成自然的中缀表达式

树中很重要的一个思想就是递归，因为树，树的子节点，等等结构都是相似的，因此同一种规律/算法就可以不断的反复套用。在遍历，插入，增删查改中都会用到递归的思想。

散列

散列的定义

散列表的实现被称为散列（Hashing）

散列是一种以常熟平均时间执行插入删除查找的技术。但是散列表中的元素之间的排列顺序是随机的，因此是无法通过线性时间来打印散列表

散列函数：其作用就是将关键字尽可能合适的映射到不同的存储单元中去。

但是毫无疑问，由于存储单元的数目是有限的而关键字的个数是无穷的，在后期的散列分配映射过程中肯定会遇到冲突现象，因此需要解决冲突。

当关键字是整数时，可以通过对单元个数取模来实现散列函数的确定，但是如果散列表的大小为10，而关键字多是以0结尾，那么这种情况下散列分配的结果就不够理想，因此，在设计散列表的大小时应该尽量采用素数大小！

解决散列冲突问题

如果当一个元素被插入时另一个元素已经存在，即两个元素的散列值相同，那么就会产生一个冲突！

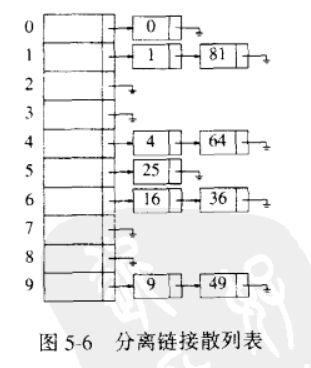
分离链接法

分离链接法的做法是将散列到同一个散列值的所有元素都保留到一个表中，并且这些表都有表头，如果空间较为局促，那也可以不使用表头

填装因子$λ$为散列表中的元素个数与散列表大小的比值

  • 装填因子Load factor $λ$=元素个数/哈希表的大小=链表的平均长度
  • 输入规模的大小不用N，而用λ
  1. 平均情况分析（λ=O(1),O(1)）
    • 不成功的查找: λ 次比较（ 1+λ ）
    • 成功查找：1+λ/2（ 1+λ ）
    • 插入：1+λ
    • 删除：1+λ/2（ 1+λ ）
  2. 最坏情况分析(λ=O(N),所有元素哈希到同一链表，O(N))
    • 不成功的查找
    • 成功查找
    • 插入
    • 删除

分离链接法的一般法则是使得表的大小尽量与预料的元素个数差不多，即尽量让$λ≈1$,是表的大小尽量是一个素数，且各个冲突处理链表尽可能短。

缺点是分离链接法浪费了大量时间在分配内存空间上。

开放定址法

在开放定址法中，不使用指针，而是用了另一种方式，它在遇到冲突时，选择在散列表中寻找其他没有被使用的单元，直到选中了空单元才停止。
$$
h_i(X) = (Hash(X)+F(i)) \mod TableSize
$$
因此开放定址法的空间需求相对分离链接法要更大一般而言$λ≤0.5$。

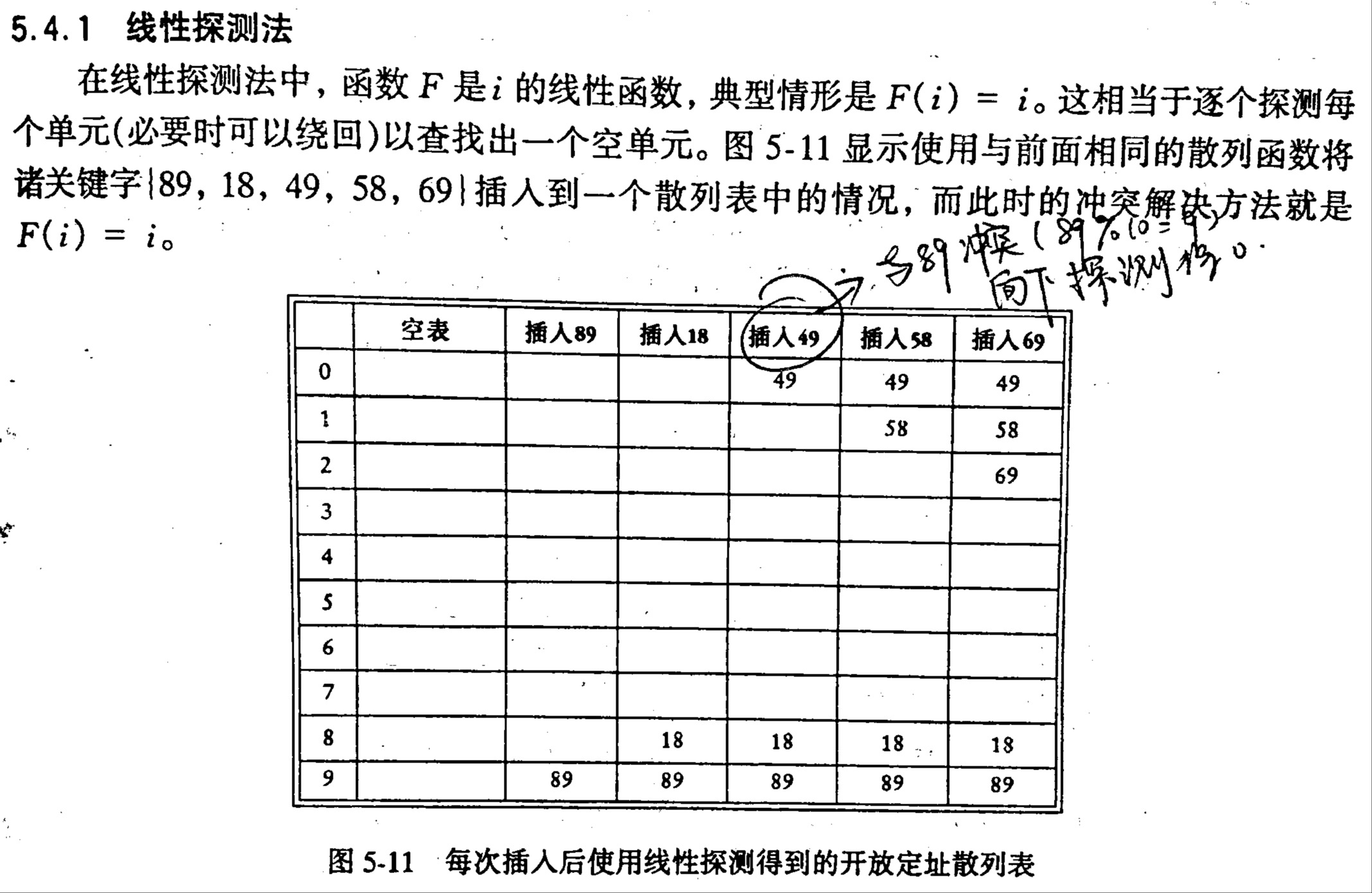
线性探测法

在线性探测法中，函数F是i的线性函数，即F的最高次数为1次，典型情况为
$$
F(i) = i
$$
这相当于逐个探测每个散列表单元，并且必要时可以返回循环遍历整个散列表直到查到一个可用的空单元。

容易看出，如果插入的关键字的散列结果较为接近，那么就会出现一次聚集现象。

如果表有超过一半可以被使用的话，那么线性探测法就是一个较好的办法，然而如果$λ = 0.5$，那么平均插入操作只需要探测2.5次，而对于成功的操作只需要探测1.5次。因此我们在使用线性探测法使应该尽量使填充因子小于0.5！

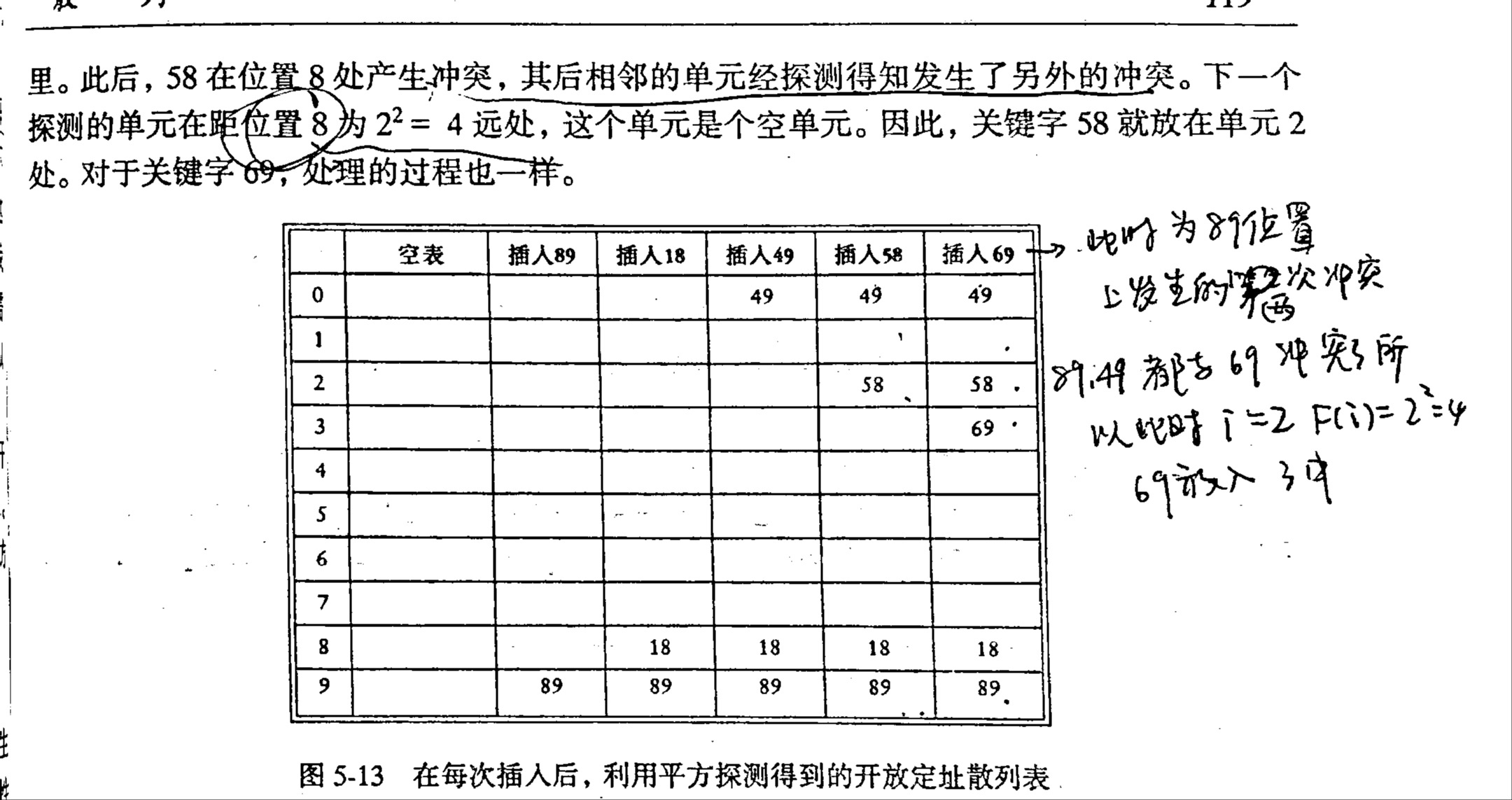
平方探测法

该方式是消除线性探测法中一次聚集问题的冲突解决办法。平方探测法的冲突函数是二次函数，其较为主流的选择为
$$
F(i) = i^2
$$

规律：使用平方探测法，当表有一半是空的时，并且表的大小为素数，那么我们总能保证此时可以插入一个新的元素。

在开放定址散列表中，标准的删除操作是无法施行的，因为相应的单元可能已经发生了冲突，其元素已经被挪到了其他位置上了。

优先队列-堆

在传统的队列结构Queue中，各个元素都是没有指定的优先级的，都遵循严格的先入先出原则，但是这样的原则并不是永远都是合适的，当我们遇到了CPU处理事件的类似问题时，就会出现优先级的考虑，优先级相对较高的问题应该更快更早被考虑和解决。

因此为了应对这个需求，我们更不应该直接使用线性结构–数组，因为如果使用数组的话最坏情况可能会达到$O(N)$,也就是需要出队的那个元素在最末尾，我们需要多次比较才能找到那个元素！于是我们应该采用二叉堆。

二叉堆

二叉堆又有最大堆与最小堆的不同类型。其分别对应了最大优先队列和最小优先队列。

二叉堆是一颗被完全填满的二叉树，但是并不是完全二叉树，它在最底层是有可能存在没有完全放满叶子的情况，因此一颗高度为h的二叉树，它的总结点数应该为：2h到2h+1-1​

并且如果用数组来存储二叉堆，其根节点与子节点有这样的性质：

  • 如果根节点为i，那么它的左儿子的下标就是2*i+1右儿子的下标就是2*i+2
  • 下标为length/2 -1的堆元素肯定存在有左儿子

二叉堆的构造

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static void heapAdjust(int[] arr,int root,int length) {
       // 以 root节点为根节点，遍历这个长度为length的数组，判断其是否满足大顶堆的要求，而且我们只需要判断根节点和其两个子节点是否满足就好了，其他的事情交给循环来做
       //这里放一个length是为了保证访问数组的时候不会越界
       int child;  // 子节点的值
       int father; // 父节点的值
       for(father = arr[root];2*root+1 < length;root = child){
           //只要它的左儿子是存在的，那么就开始构造/重构堆
           child = 2*root+1; // 以root节点为根节点的左子树的下标

           // 如果这个根节点的左子树不是这个堆的最后一个元素并且左子树小于右子树。那么就把下标指向右子树
           // 因为小的元素要下沉就必须要跟两个子树中较大的那个进行交换，否则如果跟较小的节点进行交换的话可能还需要交换两次！
           if (child != length-1 && arr[child] < arr[child+1]) {
               child++;
           }
           // 如果此时的父节点小于子树中的那个较大者，就与之交换！
           if (father < arr[child]) {
               arr[root] = arr[child]; // 父节点的原有值已经记录在father这个变量内了！
               //交换之后还需要接着对这个以儿子节点为根节点的子树进行堆判断，也就是进入下一个循环
           }else{
               // 说明该节点符合大顶堆的标准，退出for循环
               break;
           }
       }
       // 由于当前下标为root的节点值可能是废弃的，即已经被交换过，所以这个节点位置的应有值是该移动节点的值，即最初始的父节点
       arr[root] = father;
   }

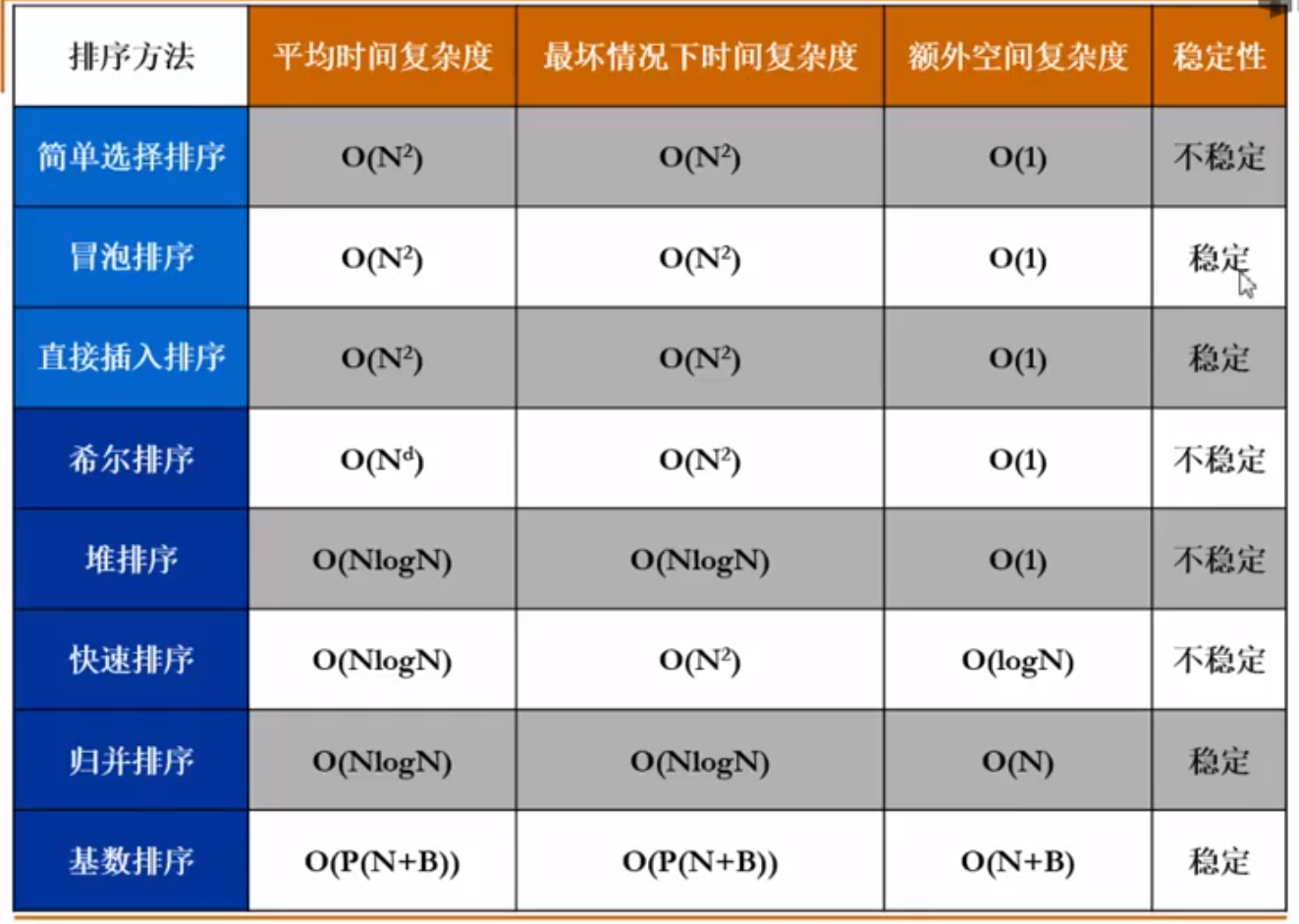
二叉堆的插入算法

排序

插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void insertSort(int A[],int length){
    // 插入排序的主要思想是排过序的前一部分是永远有序的，只需要将当前元素放置到正确位置就好
    int temp = 0;
    int j = 0;
    for (int i = 1; i < length; i++)//可以选择直接从第一个元素开始
    {
        temp = A[i];
        for (j = i; j > 0 && A[j-1] > temp; j--)// 第一个j=i的元素是还没有被排序的待排元素！所以要从第i-1个元素开始排序
        {
            A[j] = A[j-1];
        }
        // 退出上一个循环的原因要么是找到了该放的正确位置，要么是到了数组的第一位。
        // 但是不管是那种情况，此时j就是正确位置的下标！
        A[j] = temp;
    }
}

希尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void shellSort(int A[],int length){
    // int A[5] = {7,6,5,9,3};
    int temp = 0;
    int j = 0;
    for (int increment = length/2; increment > 0; increment /= 2)
    {
        for (int i = increment; i < length; i++)
        {
            temp = A[i];
            // 从下标为increment 的元素开始，由于每次的间隔已知，且开头已知，那么由后向前找较为的方便
            // 确保每个元素在这个增量间隔序列中的位置是正确的！
            for (j = i; j >= increment; j -= increment)
            {
                if (temp < A[j - increment])
                {
                    A[j] = A[j - increment];
                }else
                {
                    break;
                }
            }
            A[j] = temp;
        }
    }
}

堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
public static void main(String[] args) {
        int[] arr = { 50, 10, 90, 30, 70, 40, 80, 60, 20 };
		System.out.println("排序之前：");
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
 
		// 堆排序
		heapSort(arr);
 
		System.out.println();
		System.out.println("排序之后：");
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
    }
    public static void heapSort(int[] arr) {
        // Create a big top heap
        for (int i = arr.length/2; i >=0; i--) {
            heapAdjust(arr, i, arr.length);//从中间到开头的所有元素都进行堆的标准判断，确保生成一个完整的堆
        }
        // 将堆顶最大的那个元素和后面的元素进行交换，然后再生成大顶堆
        for (int i = arr.length-1; i >= 0; i--) {
            // 交换堆顶和队列中最后一个元素的值
            exchange(arr, 0, i);
            // 判断这个队列是否能构成大顶堆不能的话就调整
            // 这里调整的实质是：只有堆顶一个元素需要调整，因此只需要将堆顶的元素下沉到相应的位置就好了不需要调整太多元素！！
            heapAdjust(arr, 0, i);//只排序前i个元素
        }
    }
    public static void heapAdjust(int[] arr,int root,int length) {
        // 以 root节点为根节点，遍历这个长度为length的数组，判断其是否满足大顶堆的要求，而且我们只需要判断根节点和其两个子节点是否满足就好了，其他的事情交给循环来做
        //这里放一个length是为了保证访问数组的时候不会越界
        int child;  // 子节点的值
        int father; // 父节点的值
        for(father = arr[root];2*root+1 < length;root = child){
            //只要它的左儿子是存在的，那么就开始构造/重构堆
            child = 2*root+1; // 以root节点为根节点的左子树的下标

            // 如果这个根节点的左子树不是这个堆的最后一个元素并且左子树小于右子树。那么就把下标指向右子树
            // 因为小的元素要下沉就必须要跟两个子树中较大的那个进行交换，否则如果跟较小的节点进行交换的话可能还需要交换两次！
            if (child != length-1 && arr[child] < arr[child+1]) {
                child++;
            }
            // 如果此时的父节点小于子树中的那个较大者，就与之交换！
            if (father < arr[child]) {
                arr[root] = arr[child]; // 父节点的原有值已经记录在father这个变量内了！
                //交换之后还需要接着对这个以儿子节点为根节点的子树进行堆判断，也就是进入下一个循环
            }else{
                // 说明该节点符合大顶堆的标准，退出for循环
                break;
            }
        }
        // 由于当前下标为root的节点值可能是废弃的，即已经被交换过，所以这个节点位置的应有值是该移动节点的值，即最初始的父节点
        arr[root] = father;
    }
    public static void exchange(int[] arr,int began,int end) {
        int temp = arr[began];
        arr[began] = arr[end];
        arr[end] = temp;
    }

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<stdio.h>
#define Max_ 10
 
// 归并排序中的合并算法
void Merge(int array[], int left, int m, int right)
{
    int aux[Max_] = {0};  // 临时数组 （若不使用临时数组，将两个有序数组合并为一个有序数组比较麻烦）
    int i; //第一个数组索引
    int j; //第二个数组索引
    int k; //临时数组索引
    
    for (i = left, j = m+1, k = 0; k <= right-left; k++) // 分别将 i, j, k 指向各自数组的首部。
    {
        //若 i 到达第一个数组的尾部，将第二个数组余下元素复制到 临时数组中
        if (i == m+1)
        {
            aux[k] = array[j++];
            continue;
        }
        //若 j 到达第二个数组的尾部，将第一个数组余下元素复制到 临时数组中
        if (j == right+1)
        {
            aux[k] = array[i++];
            continue;
        }
        //如果第一个数组的当前元素 比 第二个数组的当前元素小，将 第一个数组的当前元素复制到 临时数组中
        if (array[i] < array[j])
        {
            aux[k] = array[i++];
        }
        //如果第二个数组的当前元素 比 第一个数组的当前元素小，将 第二个数组的当前元素复制到 临时数组中
        else
        {
            aux[k] = array[j++];
        }
    }
    
    //将有序的临时数组 元素 刷回 被排序的数组 array 中，
    //i = left , 被排序的数组array 的起始位置
    //j = 0， 临时数组的起始位置
    for (i = left, j = 0; i <= right; i++, j++)
    {
        array[i] = aux[j];
    }
}
 
// 归并排序
void MergeSort(int array[], int start, int end)
{
    // 先拆分，直到拆分到最小部分才结束，也就是只剩下一个元素的时候开始递归返回
    // 排序是在合并的时候发生的，通过下标来控制拆分后的元素位置，然后将需要排序的元素输出到临时数组中，最后重新覆盖原始数组中的元素列
    if (start < end)
    {
        int i;
        i = (end + start) / 2;
        // 对前半部分进行排序
        MergeSort(array, start, i);
        // 对后半部分进行排序
        MergeSort(array, i + 1, end);
        // 合并前后两部分
        Merge(array, start, i, end);
    }
}
 
int main()
{   //测试数据
    int arr_test[Max_] = { 8, 4, 2, 3, 5, 1, 6, 9, 0, 7 };
    MergeSort( arr_test, 0, Max_-1 );
    return 0;
}

快速排序

快排的核心思想就是哨兵，通过两个pivot来实现将所给的数组中的所有元素排序(大致排序，只按照与标兵的大小比较)，最后哨兵会和的时候就是标兵元素的正确存放地址，此时左边为小于标兵的元素，右边是大于标兵的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <stdio.h>
#include <stdlib.h>
/*****************************************************
File name：Quicksort
Author：Zhengqijun    Version:1.0    Date: 2016/11/04
Description: 对数组进行快速排序
Funcion List: 实现快速排序算法
*****************************************************/

#define BUF_SIZE 12

/**************************************************
 *函数名：display
 *作用：打印数组元素
 *参数：array - 打印的数组，maxlen - 数组元素个数
 *返回值：无
 **************************************************/
void display(int array[], int maxlen)
{
    int i;

    for (i = 0; i < maxlen; i++)
    {
        printf("%-3d", array[i]);
    }
    printf("\n");

    return;
}

/************************************
 *函数名：QuickSort
 *作用：快速排序算法
 *参数：
 *返回值：无
 ************************************/
void QuickSort(int *arr, int low, int high)
{
    if (low < high)
    {
        int i = low;
        int j = high;
        int k = arr[low];
        while (i < j)
        {
            // 此时的K就是这次快速排序的基准值
            // 通过不断地左右探测，找到大于k的放在右边，小于k的放在左边。
            // 每次只找到第一个大于或者小于k的数，然后直接交换，再去寻找另一边的元素
            while (i < j && arr[j] >= k) // 从右向左找第一个小于k的数
            {
                j--;
            }

            if (i < j)// 确保上面的循环是因为arr[i] < k而退出的也就是找到了第一个小于k的数
            {
                arr[i++] = arr[j];//然后把这个数放入到arr[i]中
            }

            while (i < j && arr[i] < k) // 从左向右找第一个大于等于k的数
            {
                i++;
            }

            if (i < j)
            {
                arr[j--] = arr[i];
            }
        }// 当i == j时就是k应该放的位置。
        // 此时左边全部都是小于k的元素，因为所有大于k的元素都被交换到当时k所在的位置了，所有大于k的元素都被放到右侧了

        arr[i] = k;

        // 递归调用
        QuickSort(arr, low, i );  // 排序k左边。排序当前数组的最低位到i位
        QuickSort(arr, i + 1, high); // 排序k右边，排序当前数组i之后的所有元素
    }
}

// 主函数
int main()
{
    int array[BUF_SIZE] = {1,5,2,4,3,4564,2345,11,23,3423,4352,0};
    int maxlen = BUF_SIZE;

    printf("排序前的数组\n");
    display(array, maxlen);

    QuickSort(array, 0, maxlen - 1); // 快速排序

    printf("排序后的数组\n");
    display(array, maxlen);

    return 0;
}

桶式排序

桶排的原理就是归类！基数排序也是类似的原理。直接将元素放入到以该元素的数值为下标的数组单元中，不过实际操作时数组单元记录的是相同大小元素的个数！而在打印的时候只需要将数组下标打印数组元素值次就好了。

Java实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
     * 桶排序
     * 
     * @param A
     * @return
     */
    public static int[] bucketSort(int[] A, int max) {
        int[] B = new int[max + 1];// 0-max 总共max+1个数
        int[] reArray = new int[A.length];
        for (int i = 0; i < A.length; i++) {
            B[A[i]]++;
        }
        int k = 0;
        for (int i = 0; i < B.length; i++) {
            for (int j = 1; j <= B[i]; j++) {
                // i 是被排序的数的大小 B[i] 是大小为i的被排序数的个数
                reArray[k] = i;
                k++;
            }
        }
        return reArray;
    }

C语言实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void bucketSort(int A[],int length,int max){
    int B[max+1];// 根据A中元素的最大值来确定B的元素个数
    memset(B,0,(max+1)*sizeof(int));//使用memset时记得引用string.h头文件
    for(int i = 0; i < length;i++){
        B[A[i]]++;
    }
    int k = 0;
   for (int i = 0; i < max+1; i++) {
        for (int j = 1; j <= B[i]; j++) {
            // i 是被排序的数的大小 B[i] 是大小为i的被排序数的个数
            A[k] = i;
            k++;
        }
    }
}

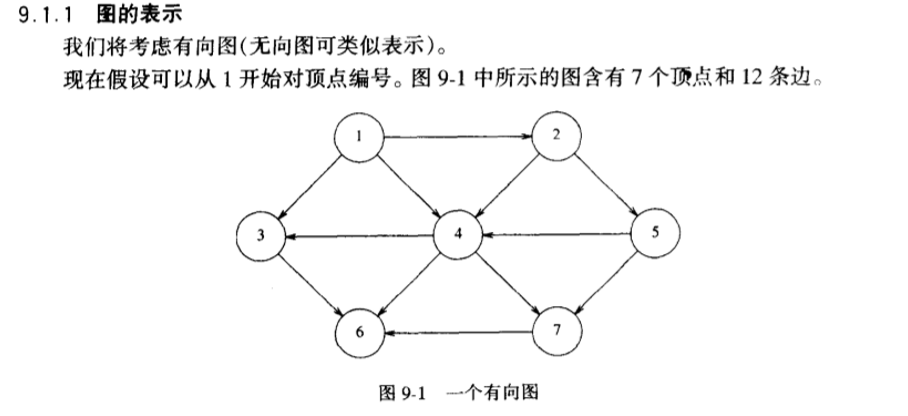
外部排序

排序分析

图论算法

图由顶点和边组成，一个图中也包含很多条边和很多个顶点。

根据边是否有向，可以将图分为有向图与无向图。

图的表示

图有两种表示形式：邻接数组和邻接表。

前者是用二维数组来实现图：

1
Graph[Vertex1][Vertex2] = weight

其中数组的两个下标为这条边的两个顶点，其中存储的值为这条边的权重

后者是用链表的方式来实现图：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#define MAX 5
typedef struct _ENode
{
    int index;                 // 该边的顶点的位置
    struct _ENode *nextEdge; // 指向下一条弧的指针
} ENode, *PENode;

// 邻接表中表的顶点
typedef struct _VNode
{
    int index;          // 顶点信息
    ENode *firstEdge; // 指向第一条依附该顶点的弧
} VNode;

// 邻接表
typedef struct _LGraph
{
    int vexNum; // 图的顶点的数目
    int edgNum; // 图的边的数目
    VNode vexs[MAX];
} LGraph;

// 边的数据
typedef struct _EData
{
    int start; // 起始顶点
    int end;   // 结束顶点
} EData;
static EData gData[] = {//硬编码的图的数据
    {0, 1},
    {0, 3},
    {1, 2},
    {1, 3},
    {2, 5},
    {3, 2},
    {3, 4}
};
void LinkToTheEnd(ENode *list, ENode *node){
    ENode *p = list;
    while (p->nextEdge)
    {
        p=p->nextEdge;
    }
    p->nextEdge = node;
    
}
// 创建一张图
LGraph *createLinkedGraph()
{
    ENode *node;
    LGraph *pG;
    int start,end;
    if ((pG = (LGraph *)malloc(sizeof(LGraph))) == NULL)
        return NULL;
    memset(pG, 0, sizeof(LGraph));
    pG->vexNum = MAX;
    pG->edgNum = 7;
    for (int i = 0; i < pG->vexNum; i++)
    {
        pG->vexs[i].index = i;
        pG->vexs[i].firstEdge = NULL;
    }
    // 初始化"邻接表"的边
    for (int i = 0; i < pG->edgNum; i++)
    {
        // 读取边的起始顶点,结束顶点
        start = gData[i].start;
        end = gData[i].end;

        // 初始化node1
        node = (ENode *)malloc(sizeof(ENode));
        memset(node,0,sizeof(ENode));
        node->index = end;
        // 将node1链接到"p1所在链表的末尾"
        if (pG->vexs[start].firstEdge == NULL)
            pG->vexs[start].firstEdge = node;
        else
            LinkToTheEnd(pG->vexs[start].firstEdge, node);
    }
    return pG;
}
int main(int argc, char const *argv[])
{
    LGraph *g;
    g = createLinkedGraph();
    return 0;
}

拓扑排序

拓扑排序的核心还是图的构建以及入度数组的维护。

只要每次都找出入度为0的顶点，然后将其输出，再更新入度数组就可以找出图的拓扑排序方式了！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#define MAX 5
typedef struct _ENode
{
    int index;                 // 该边的顶点的位置
    struct _ENode *nextEdge; // 指向下一条弧的指针
} ENode, *PENode;// _ENode 的变量别名

// 邻接表中表的顶点
typedef struct _VNode
{
    int index;          // 顶点信息
    ENode *firstEdge; // 指向第一条依附该顶点的弧
} VNode;

// 邻接表
typedef struct _LGraph
{
    int vexNum; // 图的顶点的数目
    int edgNum; // 图的边的数目
    VNode vexs[MAX];
} LGraph;

// 边的数据
typedef struct _EData
{
    int start; // 起始顶点
    int end;   // 结束顶点
} EData;
static EData gData[] = {
    {0, 1},
    {0, 3},
    {1, 2},
    {1, 3},
    {2, 4},
    {3, 2},
    {3, 4}
};
void LinkToTheEnd(ENode *list, ENode *node){
    ENode *p = list;
    while (p->nextEdge)
    {
        p=p->nextEdge;
    }
    p->nextEdge = node;
    
}
// 创建一张图
LGraph *createLinkedGraph()
{
    ENode *node;
    LGraph *pG;
    int start,end;
    if ((pG = (LGraph *)malloc(sizeof(LGraph))) == NULL)
        return NULL;
    memset(pG, 0, sizeof(LGraph));
    pG->vexNum = MAX;
    pG->edgNum = 7;
    for (int i = 0; i < pG->vexNum; i++)
    {
        pG->vexs[i].index = i;
        pG->vexs[i].firstEdge = NULL;
    }
    // 初始化"邻接表"的边
    for (int i = 0; i < pG->edgNum; i++)
    {
        // 读取边的起始顶点,结束顶点
        start = gData[i].start;
        end = gData[i].end;

        // 初始化node1
        node = (ENode *)malloc(sizeof(ENode));
        memset(node,0,sizeof(ENode));
        node->index = end;
        // 将node1链接到"p1所在链表的末尾"
        if (pG->vexs[start].firstEdge == NULL)
            pG->vexs[start].firstEdge = node;
        else
            LinkToTheEnd(pG->vexs[start].firstEdge, node);
    }
    return pG;
}
// 获取图的出度数组
void createInDegree(LGraph *g,int InDegree[]){
    ENode *p;
    for (int i = 0; i < g->vexNum; i++)
    {
        p = g->vexs[i].firstEdge;
        
        while (p)
        {
            InDegree[p->index]++;
            p = p->nextEdge;   
        }
        
    }
}
// 更新维护入度数组
/**
 * g    图指针
 * InDegree 入度数组
 * node 需要改变的节点指针
 * 删除节点后把它在入度数组中置为-1
 * */
void updateInDegree(LGraph *g,int InDegree[],int index){
    InDegree[index] = -1;
    ENode *p;
    p = g->vexs[index].firstEdge;
    while (p)
    {
        InDegree[p->index]--;
        p = p->nextEdge;   
    }
}
// TopologicalSort 拓扑排序
void TopologicalSort(LGraph *g){
    ENode *node;
    int InDegree[g->vexNum];
    memset(InDegree,0,sizeof(int)*g->vexNum);
    createInDegree(g,InDegree);
    while (1)
    {
        int j = -1;
        for (int i = 0; i < g->vexNum; i++)
        {
            if (InDegree[i] == 0)
            {
                j = i;
                break;
            }
        }
        if (j == -1)
        {
            break;
        }
        
        printf("%d",j);
        updateInDegree(g,InDegree,j);
    }
}
int main(int argc, char const *argv[])
{
    LGraph *g;
    g = createLinkedGraph();
    TopologicalSort(g);
    return 0;
}

最短路径

图的搜索方法

  • 宽度优先BFS（breath-first-search）–队列实现

    逐层遍历

    访问节点v，再依次访问和v邻接的节点（或v的下一层节点）

  • 深度优先DFS（depth-first-search）–堆栈实现：递归

    先序遍历

    访问节点v，对v的邻接节点递归DFS

Dijkstra算法

求两个顶点间的最短路径，是一种贪婪算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
import java.util.*;
public class Dijkstra {
    //定义顶点Vertex类
    static class Vertex{
        private final static int infinite_dis = Integer.MAX_VALUE;
        private String name;   //节点名字
        private boolean known;  //此节点是否已知  
        private int adjuDist;   //此节点距离  
        private Vertex parent;   //当前从初始化节点到此节点的最短路径下的父亲节点
        public Vertex(){
            this.known = false;
            this.adjuDist = infinite_dis;
            this.parent = null;
        }
        public Vertex(String name){
            this();
            this.name = name;
        }
        public Vertex getParent(){
            return parent;
        }
        public void setParent(Vertex parent){
            this.parent = parent;
        }
        public boolean equals(Object obj){
            if (this.getName() == ((Vertex)obj).getName()) {
                return true;
            }
            if(this.name == null){
                throw new NullPointerException("name of Vertex to be compared cannot be null!");
            }else{
                return false;
            }
        }
    }
    static class Edge{
        //此有向边的起始点
        private Vertex startVertex;
        //此有向边的终点
        private Vertex endVertex;
        //此有向边的权值
        private int weight;
        public Edge(Vertex startVertex,Vertex endVertex,int weight){
            this.startVertex = startVertex;
            this.endVertex = endVertex;
            this.weight = weight;
        }
        
    }
    private List<Vertex> vertexList; //图的顶点集
    private Map<Vertex,List<Edge> > ver_edgeList_map;  //图的每个顶点对应的有向边
    public Dijkstra(List<Vertex> vertexList, Map<Vertex, List<Edge>> ver_edgeList_map) {
        this.vertexList = vertexList;
        this.ver_edgeList_map = ver_edgeList_map;
    }
    public void setRoot(Vertex v){
        v.setParent(null);
        v.setAdjuDist(0);
    }
    private void updateChildren(Vertex v){
        if (v==null){
            return;
        }
        if (ver_edgeList_map.get(v)==null || ver_edgeList_map.get(v).size()==0){
            return;
        }
        List<Vertex> childrenList = new LinkedList<Vertex>();
        for (Edge e:ver_edgeList_map.get(v)){
            Vertex childVertex = e.getEndVertex();
            if (!childVertex.isKnown()){
                childVertex.setKnown(true);
                childVertex.setAdjuDist(v.getAdjuDist()+e.getWeight());
                childVertex.setParent(v);
                childrenList.add(childVertex);
            }
            int nowDist = v.getAdjuDist() + e.getWeight();
            if (nowDist >= childVertex.getAdjuDist()){
                continue;
            }else {
                childVertex.setAdjuDist(nowDist);
                childVertex.setParent(v);
            }
        }
        for (Vertex vc:childrenList){
            updateChildren(vc);
        }
    }
    
    public void dijkstraTravasal(int startIndex,int destIndex){

            Vertex start = vertexList.get(startIndex);
            Vertex dest  = vertexList.get(destIndex);
            String path = "[" + dest.getName() + "]";

            setRoot(start);

            updateChildren(vertexList.get(startIndex));

            int shortest_length = dest.getAdjuDist();

            while ((dest.getParent()!=null)&&(!dest.equals(start))){
                path = "[" + dest.getParent().getName() +"] --> "+path;
                dest = dest.getParent();
            }


        System.out.println("["+vertexList.get(startIndex).getName()+"] to ["+
                vertexList.get(destIndex).getName()+"] dijkstra shortest path:: "+path);

        System.out.println("shortest length::" + shortest_length);
    }
    public static void main(String[] args) {

        Vertex v1= new Vertex("v1");
        Vertex v2= new Vertex("v2");
        Vertex v3= new Vertex("v3");
        Vertex v4= new Vertex("v4");
        Vertex v5= new Vertex("v5");
        Vertex v6= new Vertex("v6");
        Vertex v7= new Vertex("v7");
        List<Vertex> verList = new LinkedList<Dijkstra.Vertex>();
        verList.add(v1);
        verList.add(v2);
        verList.add(v3);
        verList.add(v4);
        verList.add(v5);
        verList.add(v6);
        verList.add(v7);

        Map<Vertex, List<Edge>> vertex_edgeList_map = new HashMap<Vertex, List<Edge>>();

        List<Edge> v1List = new LinkedList<Dijkstra.Edge>();
        v1List.add(new Edge(v1,v2,2));
        v1List.add(new Edge(v1,v4,1));
        List<Edge> v2List = new LinkedList<Dijkstra.Edge>();
        v2List.add(new Edge(v2,v4,3));
        v2List.add(new Edge(v2,v5,10));
        List<Edge> v3List = new LinkedList<Dijkstra.Edge>();
        v3List.add(new Edge(v3,v1,4));
        v3List.add(new Edge(v3,v6,5));

        List<Edge> v4List = new LinkedList<Dijkstra.Edge>();
        v4List.add(new Edge(v4,v3,2));
        v4List.add(new Edge(v4,v5,2));
        v4List.add(new Edge(v4,v6,8));
        v4List.add(new Edge(v4,v7,4));

        List<Edge> v5List = new LinkedList<Dijkstra.Edge>();
        v5List.add(new Edge(v5,v7,6));

        List<Edge> v6List = new LinkedList<Dijkstra.Edge>();

        List<Edge> v7List = new LinkedList<Dijkstra.Edge>();
        v7List.add(new Edge(v7,v6,1));
        vertex_edgeList_map.put(v1, v1List);
        vertex_edgeList_map.put(v2, v2List);
        vertex_edgeList_map.put(v3, v3List);
        vertex_edgeList_map.put(v4, v4List);
        vertex_edgeList_map.put(v5, v5List);
        vertex_edgeList_map.put(v6, v6List);
        vertex_edgeList_map.put(v7, v7List);
        
        Dijkstra g = new Dijkstra(verList, vertex_edgeList_map);
        g.dijkstraTravasal(0, 6);
    }
}

C语言实现Dijkstra算法：Dijkstra

最小生成树

Prim算法

求图的最小生成树

Prim算法选取新的一条边的原则是其中一个节点必须在已经选取的节点集合中，而另一个节点必须是为选取的节点。最终选定的边还必须要是全部满足条件的未选取边的权值最小值。也就是说prim算法选取的边必须是连续的，不可能是独立的一条边，因为其中的一个顶点必定是已知的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
public class Prims {
    private static int INF = Integer.MAX_VALUE;
    private class ENode {
        int ivex;       // 该边所指向的顶点的位置
        int weight;     // 该边的权
        ENode nextEdge; // 指向下一条弧的指针
    }
    private class VNode {
        char data;          
        ENode firstEdge;    
    };
    private VNode[] mVexs;  
    public Prims(char[] vexs, EData[] edges) {
        int vlen = vexs.length;
        int elen = edges.length;
        mVexs = new VNode[vlen];
        for (int i = 0; i < mVexs.length; i++) {
            mVexs[i] = new VNode();
            mVexs[i].data = vexs[i];
            mVexs[i].firstEdge = null;
        }
        // 初始化"边"
        for (int i = 0; i < elen; i++) {
            // 读取边的起始顶点和结束顶点
            char c1 = edges[i].start;
            char c2 = edges[i].end;
            int weight = edges[i].weight;

            // 读取边的起始顶点和结束顶点
            int p1 = getPosition(c1);
            int p2 = getPosition(c2);
            // 初始化node1
            ENode node1 = new ENode();
            node1.ivex = p2;
            node1.weight = weight;
            // 将node1链接到"p1所在链表的末尾"
            if(mVexs[p1].firstEdge == null)
                mVexs[p1].firstEdge = node1;
            else
                linkLast(mVexs[p1].firstEdge, node1);
            // 初始化node2
            ENode node2 = new ENode();
            node2.ivex = p1;
            node2.weight = weight;
            // 将node2链接到"p2所在链表的末尾"
            if(mVexs[p2].firstEdge == null)
                mVexs[p2].firstEdge = node2;
            else
                linkLast(mVexs[p2].firstEdge, node2);
        }
    }
    private void linkLast(ENode list, ENode node) {
        ENode p = list;
        while(p.nextEdge!=null)
            p = p.nextEdge;
        p.nextEdge = node;
    }
    private int getPosition(char ch) {
        for(int i=0; i<mVexs.length; i++)
            if(mVexs[i].data==ch)
                return i;
        return -1;
    }
    private int getWeight(int start, int end) {

        if (start==end)
            return 0;

        ENode node = mVexs[start].firstEdge;
        while (node!=null) {
            if (end==node.ivex)
                return node.weight;
            node = node.nextEdge;
        }

        return INF;
    }
    public void prim(int start) {
        int min,i,j,k,m,n,tmp,sum;
        int num = mVexs.length;
        int index=0;                   // prim最小树的索引，即prims数组的索引
        char[] prims = new char[num];  // prim最小树的结果数组
        int[] weights = new int[num];  // 顶点间边的权值
        prims[index++] = mVexs[start].data;
        for (i = 0; i < num; i++ )
            weights[i] = getWeight(start, i);

        for (i = 0; i < num; i++) {
            if(start == i)
                continue;
            j = 0;
            k = 0;
            min = INF;
            while (j < num) {
                if (weights[j] != 0 && weights[j] < min) {
                    min = weights[j];
                    k = j;
                }
                j++;
            }
            prims[index++] = mVexs[k].data;
            weights[k] = 0;
            for (j = 0 ; j < num; j++) {
                tmp = getWeight(k, j);
                if (weights[j] != 0 && tmp < weights[j])
                    weights[j] = tmp;
            }
        }
        sum = 0;
        for (i = 1; i < index; i++) {
            min = INF;
            n = getPosition(prims[i]);
            for (j = 0; j < i; j++) {
                m = getPosition(prims[j]);
                tmp = getWeight(m, n);
                if (tmp < min)
                    min = tmp;
            }
            sum += min;
        }
        System.out.printf("PRIM(%c)=%d: ", mVexs[start].data, sum);
        for (i = 0; i < index; i++)
            System.out.printf("%c ", prims[i]);
        System.out.printf("\n");
    }
    private static class EData {
        char start; // 边的起点
        char end;   // 边的终点
        int weight; // 边的权重

        public EData(char start, char end, int weight) {
            this.start = start;
            this.end = end;
            this.weight = weight;
        }
    };

   public static void main(String[] args) {
       char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
       EData[] edges = {
               new EData('A', 'B', 12),
               new EData('A', 'F', 16),
               new EData('A', 'G', 14),
               new EData('B', 'C', 10),
               new EData('B', 'F',  7),
               new EData('C', 'D',  3),
               new EData('C', 'E',  5),
               new EData('C', 'F',  6),
               new EData('D', 'E',  4),
               new EData('E', 'F',  2),
               new EData('E', 'G',  8),
               new EData('F', 'G',  9),
       };
       Prims pG;
       pG = new Prims(vexs, edges);
       pG.prim(0);   // prim算法生成最小生成树
   }
}

Kruskal算法

这个算法也是一个最小生成树算法。不过它与上面的Prim算法有所不同。

Prim算法选取新的一条边的原则是其中一个节点必须在已经选取的节点集合中，而另一个节点必须是为选取的节点。最终选定的边还必须要是全部满足条件的未选取边的权值最小值。也就是说prim算法选取的边必须是连续的，不可能是独立的一条边，因为其中的一个顶点必定是已知的。

Kruskal算法是在所有的边中进行。先排序，找出未加入生成树的最小权值的边，然后判断其是否会与已选取的边构成环，如果不会那么就加入到生成树中。

很显然这个算法也是一个贪婪算法。

算法设计技巧

NP完全问题：NP也就是Non-deterministic Polynomial的缩写，非确定性多项式。

多项式时间指的是是时间复杂度为：$O(N)$ ,$O(\log(N))$等

非多项式时间是指这类算法的时间复杂度已经超过了计算机能够承受的范围了，例如$O(N!)$一类的时间复杂度。

贪婪算法

贪婪算法是将任务分成不同的阶段，在每一个可以快速简单寻找到当前最优解的片段中，取用最优解，然后对每一个片段都重复这个过程，最终得到的就是整个任务的最优解或是次优解。

图例

其中的平均完成时间的定义是：完成该任务的时间节点，而不是完成该任务的时间长度！

所以10-2为：
$$
(15+23+26+36)/4 = 25
$$
10-3为:
$$
(3+11+21+36)/4 = 17.75
$$
因此可以表明，不是是用事件单调递减的序列的解决方案必然是次优解，只有那些最小运行时间任务最先安排的解决办法才是最优解。

贪婪算法的应用

  • 寻找图中的最短路径–Dijkstra算法
  • 寻找图的最小生成树–Prim算法
  • 还有就是文件压缩–Huffman编码

Huffman编码

由此可以得到字符编码的前缀码，不过使用前缀码的前提是每个字符编码都不是其他编码的前缀！因此每个字符都要放在树的叶子节点上。

这样做就确保了编码没有二义性。

编码的比特数：

其中深度的数值等于其编码的位数！

Huffman算法

算法对一个由树组成的森林进行，该森林中一共有C片叶子，也就是有C个字符需要编码。一棵树的权重等于它的树叶的频率之和。任取最小权重的两棵树$T_1$,$T_2$,并以这两棵树为子树形成新的树，将这样的过程进行C-1次，最终得到的就是Huffman编码的最优树。

为什么需要进行C-1次：

​ 因为森林中最开始有C棵树，也就是一共有C棵只有一个节点的树，每一次选取都会让两棵树合并成一棵树，树的总数减少一，因此从C到1也就需要进行C-1次

示例图：

该算法每一次选取子树都是在当前条件下选取权重最小的子树，因此该算法是贪婪算法。

代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <stdfix.h>
/***
 * 哈夫曼编码树
 * */
typedef struct HuffmanTree
{
    char con[2];                       // 节点的内容
    int f;                          //节点的频率
    struct HuffmanTree *leftChild;  //左儿子
    struct HuffmanTree *rightChild; //右儿子
} * Node;
// 创建一个新的节点
Node createNode(char con[], int f, Node left, Node right)
{
    // 先创建一个指针
    Node newNode;
    if ((newNode = (Node)malloc(sizeof(Node))) == NULL)
    {
        return NULL;
    }
    memset(newNode, 0, sizeof(Node));
    // strcpy(newNode->con,con);
    if (con)
    {
        memcpy(newNode->con,con,2*sizeof(char));
    }else
    {
        memset(newNode->con,0,2*sizeof(char));
    }
    // newNode->con = con;
    newNode->f = f;
    newNode->leftChild = left;
    newNode->rightChild = right;
    return newNode;
}
/**
 * tree 树的数组
 * legth 数组的长度
 * */
Node huffman(Node tree[], int length)
{
    Node tempNode, node1, node2,parent;
    //如果这个数组里面只剩下了两个元素，那么就说明已经排序完成了
    if (length == 2)
    {   
        node1 = tree[0];
        node2 = tree[1];
        parent = createNode(NULL,node1->f+node2->f,node1,node2);
        return parent;
    }
    
    // 给这个节点数组排序，找出频率最小的两个点
    int j = 0;
    for (int i = 0; i < length; i++)
    {
        tempNode = tree[i];
        for (j = i; j > 0 && tempNode->f < tree[j - 1]->f; j--)
        {
            tree[j] = tree[j - 1];
        }
        tree[j] = tempNode;
    }
    // 频率最小的两个节点
    node1 = tree[0];
    node2 = tree[1];
    parent = createNode(NULL,node1->f+node2->f,node1,node2);
    // 重新构建一个数组
    Node newArray[length-1];
    for (int i = 0; i < length - 2; i++)
    {
        newArray[i] = tree[i+2];
    }
    newArray[length-2] = parent;
    parent = huffman(newArray,length-1);
    return parent;
}

int main(int argc, char const *argv[])
{
    Node node_a, node_e, node_i, node_s, node_t, node_sp, node_nl,result;
    node_a = createNode("a", 10, NULL, NULL);
    node_e = createNode("e", 15, NULL, NULL);
    node_i = createNode("i", 12, NULL, NULL);
    node_s = createNode("s", 3, NULL, NULL);
    node_t = createNode("t", 4, NULL, NULL);
    node_sp = createNode("sp", 13, NULL, NULL);
    node_nl = createNode("nl", 1, NULL, NULL);
    Node nodeArray[] = {node_a, node_e, node_i, node_s, node_t, node_sp, node_nl};
    result = huffman(nodeArray, 7);
    return 0;
}

分治算法

  • 分(Divide):递归解决较小的问题，基本情况直接返回就好
  • 治(Conquer):从子问题中重构原问题的解
应用

动态规划

动态规划的核心思想是

将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

斐波那契数列动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
int fib(int n){
    int f1,f2;
    f1 = f2 = 1;
    int result = 1;
    if (n < 3)
    {
        return f1;
    }
    for (int i = 2; i < n; i++)
    {
        result = f1 + f2;
        f1 = f2;
        f2 = result; 
    }
    return result;
}
int main(int argc, char const *argv[])
{
    fib(8);
    return 0;
}

最短编辑距离

在有的文章中，替换的代价是2，而在有的文章中，替换的代价是1，本文按照代价为1的来计算。不过个人认为代价为二更加合理。

动态规划表的初始化
  • D(0,j)=j，空串和长度为j的Y子串间的最小编辑距离（添加或删除对应的次数）
  • D(i,0)=i，长度为i的X子串和空串间的最小编辑距离添加或删除对应的次数）

而最终的表的结果是：

在三个中取最小值作为矩阵的元素！也就是为了找出变成另一个字符串的最小代价

举例
· s n o w y
· 0 1 2 3 4 5
s 1 0 1 2 3 4
u 2 1 1 2 3 4
n 3 2 1 2 3 4
n 4 3 2 2 3 4
y 5 4 3 3 3 3

所以最终的结论是sunny到snowy的最小编辑距离为3 。

· a m e
· 0 1 2 3
m 1 1 1 2
e 2 2 2 1

所以最终的结论是me到ame的最小编辑距离为1 。

下面是源码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define min(a, b) (a < b ? a : b)
#define MAX 10
/**
 * res 字符1--原始字符串
 * des 字符2--目标字符串
 * 
 * */
int minEditDistance(char *res, char *des)
{
    //首先初始化动态表--填充相对于空字符的编辑距离，也就是字符长度
    int dis[MAX][MAX] = {0};
    for (int i = 1; i <= (int)strlen(des); i++)
    {
        dis[0][i] = i;
    }
    for (int j = 1; j <= (int)strlen(res); j++)
    {
        dis[j][0] = j;
    }
    //循环遍历整个数组，计算每一个编辑距离
    for (int i = 1; i <= (int)strlen(res); i++)
    {
        for (int j = 1; j <= (int)strlen(des); j++)
        {
            // 如果在该位置的两个元素相同，那么到此的最小编辑距离就等同于不包含这两个元素的最小编辑距离
            if (res[i-1] == des[j-1])
            {
                dis[i][j] = dis[i-1][j-1];
            }
            else
            {
                /**
                 * 相对而言的！向下走的意思就是多出了一个多余元素，在相对于上面那一格的最小编辑距离而言需要将这个多出来的元素删掉
                 * 同理，向右走就是目标串多了一个元素，要在左侧编辑的基础下再多加一个元素
                 * 向右下角走也是差不多的道理，既有一个多余元素，而且目标串也多了一个元素，所以要使用替换操作。
                 * */
                int delEd = dis[i][j-1]+1;//往下走就是删除 
                int insEd = dis[i-1][j]+1;//往右走是插入
                int subEd = dis[i-1][j-1]+1;//向右下角走--对角线走就是替换 在这里替换的代价是1

                int minEd = min(min(delEd,insEd),subEd);
                dis[i][j] = minEd;
            }
        }
    }
    for(int m = 0; m < MAX; m++){
        for(int n = 0; n < MAX; n++){
            printf("%d",dis[m][n]);
        }
        printf("\n");
    }
    return dis[(int)strlen(res)][(int)strlen(des)];
}

int main(int argc, char const *argv[])
{
    printf("Min Distance of %s to %s is %d \n","sunny","snowy",minEditDistance("sunny","snowy"));
    printf("Min Distance of %s to %s is %d","me","ame",minEditDistance("me","ame"));
    return 0;
}

数据结构入门？这一篇就够了

https://www.tanknee.cn/2019/11/28/datastruct_review/

作者

TankNee

发布于

11/28/2019

更新于

06/17/2022

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

最新文章

分类

×