算法分析入门系列(一) 排序算法

排序算法

main函数代码

public static void main(String[] args) {
    int max = 10;
    System.out.println("插入排序-------------------------------------");
    int[] num = randomCreate(max);
    printResult(num);
    Long bt = System.nanoTime();
    int[] temp1 = insertSort(num);
    Long et = System.nanoTime();
    System.out.println("排序用时：" + (et - bt + ""));
    printResult(temp1);


    System.out.println("合并排序-------------------------------------");
    int[] temp4 = randomCreate(max);
    printResult(temp4);
    Long bt2 = System.nanoTime();
    mergeSort(temp4);
    Long et2 = System.nanoTime();
    System.out.println("排序用时：" + (et2 - bt2 + ""));
    printResult(temp4);


    System.out.println("快速排序-------------------------------------");
    int[] temp5 = randomCreate(max);
    printResult(temp5);
    Long bt3 = System.nanoTime();
    quickSort(temp5, 0, temp5.length - 1, false);
    Long et3 = System.nanoTime();
    System.out.println("排序用时：" + (et3 - bt3 + ""));
    printResult(temp5);

    System.out.println("随机化快速排序--------------------------------");
    int[] temp9 = randomCreate(max);
    printResult(temp9);
    Long bt7 = System.nanoTime();
    quickSort(temp9, 0, temp9.length - 1, true);
    Long et7 = System.nanoTime();
    System.out.println("排序用时：" + (et2 - bt2 + ""));
    printResult(temp9);


    System.out.println("桶排序---------------------------------------");
    int[] temp6 = randomCreate(max);
    printResult(temp6);
    Long bt4 = System.nanoTime();
    temp6 = bucketSort(temp6, max);
    Long et4 = System.nanoTime();
    System.out.println("排序用时：" + (et4 - bt4 + ""));
    printResult(temp6);

    System.out.println("计数排序-------------------------------------");
    int[] temp7 = randomCreate(max);
    printResult(temp7);
    Long bt5 = System.nanoTime();
    temp7 = countSort(temp7);
    Long et5 = System.nanoTime();
    System.out.println("排序用时：" + (et5 - bt5 + ""));
    printResult(temp7);

    System.out.println("基数排序-------------------------------------");
    int[] temp8 = randomCreate(max);
    printResult(temp8);
    Long bt6 = System.nanoTime();
    radixSort(temp8, (max + "").length());
    Long et6 = System.nanoTime();
    System.out.println("排序用时：" + (et6 - bt6 + ""));
    printResult(temp8);
    System.out.println("---------------------------------------------");

}

各个排序的源代码：

插入排序：

/**
 * 插入排序
 * 
 * @param A
 * @return
 */
public static int[] insertSort(int[] A) {
    int temp = 0;
    for (int i = 1; i < A.length; i++) {
        /**
         * 将当前的数存储起来用来在0-i+1的区间内进行排序
         */
        temp = A[i];
        for (int j = i; j > 0; j--) {
            if (temp < A[j - 1]) {
                A[j] = A[j - 1];
            } else {
                A[j] = temp;
                break;
            }
            if (j - 1 == 0) {
                A[0] = temp;
            }
        }
    }
    return A;
}

合并排序：

/**
     * 合并排序
     * 
     * @param original
     */
    private static void mergeSort(int[] original) {
        if (original == null) {
            throw new NullPointerException("The array can not be null !!!");
        }
        int length = original.length;
        if (length > 1) {
            int middle = length / 2;
            int partitionA[] = Arrays.copyOfRange(original, 0, middle);// 拆分问题规模
            int partitionB[] = Arrays.copyOfRange(original, middle, length);
            // 递归调用
            mergeSort(partitionA);
            mergeSort(partitionB);
            sort(partitionA, partitionB, original);
        }
    }

    private static void sort(int[] partitionA, int[] partitionB, int[] original) {
        int i = 0;
        int j = 0;
        int k = 0;
        while (i < partitionA.length && j < partitionB.length) {
            if (partitionA[i] <= partitionB[j]) {
                original[k] = partitionA[i];
                i++;
            } else {
                original[k] = partitionB[j];
                j++;
            }
            k++;
        }
        if (i == partitionA.length) {
            while (k < original.length) {
                original[k] = partitionB[j];
                k++;
                j++;
            }
        } else if (j == partitionB.length) {
            while (k < original.length) {
                original[k] = partitionA[i];
                k++;
                i++;
            }
        }
    }

快速排序与随机快速排序：

/**
     * 快速排序
     * @param arr 数组
     * @param low 最低位
     * @param high 最高位
     * @param random 是否随机化
     */
public static void quickSort(int[] arr, int low, int high, boolean random) {
        int i, j, temp, t;
        if (low > high) {
            return;
        }
        i = low;
        j = high;
        // 以第一位为分割中心
        if (!random) {
            temp = arr[low];
        } else {
            int index = (int) Math.random() * high;
            temp = arr[index];
            arr[index] = arr[low];
            arr[low] = temp;
        }


        while (i < j) {
            //先看右边，依次往左递减
            while (temp <= arr[j] && i < j) {
                j--;
            }
            //再看左边，依次往右递增
            while (temp >= arr[i] && i < j) {
                i++;
            }
            //如果满足条件则交换
            if (i < j) {
                t = arr[j];
                arr[j] = arr[i];
                arr[i] = t;
            }

        }
        //最后将基准为与i和j相等位置的数字交换
        arr[low] = arr[i];
        arr[i] = temp;
        //递归调用左半数组
        quickSort(arr, low, j - 1, random);
        //递归调用右半数组
        quickSort(arr, j + 1, high, random);
    }

桶排序：

/**
     * 桶排序
     * 
     * @param A
     * @return
     */
    public static int[] bucketSort(int[] A, int max) {
        int[] B = new int[max + 1];// 0-max 总共max+1个数
        int[] reArray = new int[A.length];
        for (int i = 0; i < A.length; i++) {
            B[A[i]]++;
        }
        int k = 0;
        for (int i = 0; i < B.length; i++) {
            for (int j = 1; j <= B[i]; j++) {
                // i 是被排序的数的大小 B[i] 是大小为i的被排序数的个数
                reArray[k] = i;
                k++;
            }
        }
        return reArray;
    }

计数排序

/**
    * 计数排序
    *
    * @param array
    */
   public static int[] countSort(int[] array) {
       // 首先为所有元素申请足够大的空间
       int max = array[0];
       int min = array[0];
       for (int i = 0; i < array.length; i++) {
           if (max < array[i]) max = array[i];
           if (min > array[i]) min = array[i];
       }
       int maxLength = max - min + 1;
       int[] timesAndPosition = new int[maxLength];
       int[] finalArray = new int[array.length];
       for (int i = 0; i < array.length; i++) {
           timesAndPosition[array[i] - min] += 1;
       }
       for (int i = 1; i < maxLength; i++) {
           timesAndPosition[i] += timesAndPosition[i - 1];
       }
       for (int i = 0; i < array.length; i++) {
           try {
               int tempIndex = array[i] - min;
               finalArray[timesAndPosition[tempIndex] - 1] = array[i];
               timesAndPosition[tempIndex]--;
           } catch (Exception e) {
               e.printStackTrace();
           }

       }
       return finalArray;
   }

基数排序

/**
     * 基数排序
     *
     * @param array 待排序的数组
     * @param max   数组中最大数的位数
     */
    public static void radixSort(int[] array, int max) {
        List<Integer>[] temp = new List[10];
        for (int i = 0; i < temp.length; i++) {
            temp[i] = new ArrayList<>();
        }
        for (int k = 1; k <= max; k++) {
            for (int i = 0; i < temp.length; i++) {
                temp[i] = new ArrayList<>();
            }
            for (int i = 0; i < array.length; i++) {
                temp[getFigure(array[i], k)].add(array[i]);
            }
            int j = 0;
            for (int i = 0; i < temp.length; i++) {
                for (int t : temp[i]) {
                    array[j] = t;
                    j++;
                }
            }
        }
    }
 /**
     * 获取整型数的第k位的数字
     *
     * @param num 数字
     * @param k   第k位
     * @return
     */
    public static int getFigure(int num, int k) {
        // 先除以10的k-1次方，将需要获取的那位数移动到最后一位上，然后和10取余数，得到该位数
        return (num / ((int) Math.pow(10, k - 1))) % 10;
    }

随机数生成函数与打印函数：

/**
     * 随机数生成函数
     * 
     * @param num
     * @return
     */
    public static int[] randomCreate(int num) {
        int[] array = new int[num];
        for (int i = 0; i < num; i++) {
            array[i] = (int) (Math.random() * num);
        }
        return array;
    }
/**
     * 循环打印结果
     *
     * @param arr
     */
    public static void printResult(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]);
            System.out.print(" ");
        }
        System.out.println();
    }

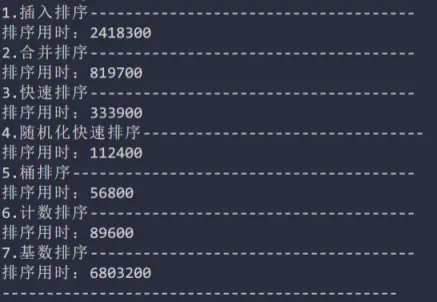
实验结果

单位：ns

实验过程

使用上文中的随机数生成函数生成1000个随机数字，然后再运行对应的排序算法，计时器使用的是Java原生的System.nanoTime();

思考题

1. 算法科学解决问题的一般模式是什么？

• 用自然语言的方式描述问题
• 抽象问题的共性，分析问题的特性
• 选用或者创建合适的数据结构模型
• 编写算法

2. 确定性算法和随机性算法的差异在那里？随机化对于算法效率的影响如何？

• 确定性算法对于随机情况是不稳定的，而随机性算法对于一般的随机情况而言更加的适用。当遇上极端情况时确定性算法就有可能不再适用而随机算法的随机化过程能较大程度的减少极端情况的影响。
• 能够普遍地提高算法的效率。如在随机化快速排序中，通过基准节点的随机化选择，就能较好的避免已经排好序/逆序的情况下的低效率。

3. 如何理解算法效率分析的渐近特征和相对性？

• 因为算法每次面对的信息量都不相同，所以就不能用一个准确的值去描述算法的绝对效率，于是就应该选择相对的N，也就是每个元操作（此处是我给出的概念，也就是抽象认知下不可分割的最小操作节点），单次元操作记作1，所有元操作的和最大值就是该算法的上界。
• 同样的，因为数据量的不尽相同，所以最终的效率只能逼近靠近理论的算法效率，也就是渐近特征